Use voltmeter, ammeter, wattmeter to determine active, reactive and apparent power
consumed in given R-L-C series circuit. Draw phasor diagram

Experiment No.: 4

Experiment Name:

Use of Voltmeter, Ammeter, Wattmeter to Determine Active, Reactive and Apparent Power
Consumed in Given R-L-C Series Circuit and Draw Phasor Diagram.

Objective:

1. To use voltmeter, ammeter, wattmeter to determine active, reactive and apparent power
   consumed in given R-L-C series circuit.
2. To draw the phasor diagram of that circuit.

Theory:

Let V volts (rms) be applied to an R-L-C series circuit and the current flowing through the circuit be I amps. The impedance Z=V/I. If voltage across resistor is V_R then R=V_R/I

If voltage across inductor is _{V r,L,} the impedance of the inductor coil is given by

V_r,_L/I=√(r²+X_L²)

Again the voltage across the resistance R and coil V_{R, L}, then

V_r,_L/I=√((R+r)²+X_L² )

From the above two equation the value of R and X_L can be found out. If the voltage across the capacitor is V_C then the reactance of the capacitor is given by X_C=V_C/I. hence the value of capacitance C=1/ωV_C where ω=2πf is the angular frequency. the power factor is given by (R+r)/Z. If V_C>V_L, The pf is leading otherwise lagging.

The power consumed P=I²(R+r) or VI cos Ø

Circuit Diagram:

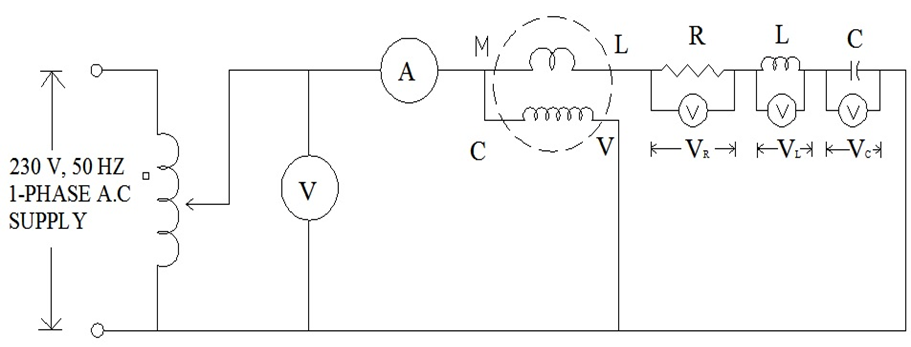
Procedure:

1. The circuit is connected as shown in the circuit diagram with resistor, the inductor coil and capacitor in series.
2. The variac is adjusted to zero output position and the circuit is switched on.
3. A suitable voltage is applied from the variac so that a reasonable current flows through the circuit. The output voltage of the variac and voltage across the resistor, inductor and the capacitor are noted along with the current.
4. Different readings are taken by varying voltage from the variac.
5. Readings are noted from the data sheet.

Observation Table:

Sl no	Voltage (V)	Current (mA)	Frequency (kHz)	R (Ω)	L (mH)	C (nF)	VR (V)	VR (V)	VC (V)	PF = cos Ø	Active power (mW) [VIcosØ]	Reactive power (mVAR) [VIsinØ]	Apparent power (mVA) [VI]
1.	5.02	9.09	13.05	546	7.75	22.08	4.67	4.22	4.2	0.98	44.71	9.034	45.62

Calculation:

X_L = 2πfL = 2π×13.05×10³×7.75×10^-3= 635.46 Ω

X_C = 1/2πfC = 1/(2π×13.05×10³×22.08×10^-9)= 552.34 Ω

cos Ø = R/Z = R/√(R²+(X_L – X_C)²) = 546/√(546²+(635.46 – 552.34)²) = 546/552.29 = 0.98 lag

Active power = VIcosØ = 5.02×9.09×10^-3×0.98 = 44.71 mW

Rective power = VIsinØ = 5.02×9.09×10^-3×0.198 = 9.034 mVAR

Apparent power = VI = 5.02×9.09×10^-3 = 45.62 mVA

Phasor Diagram:

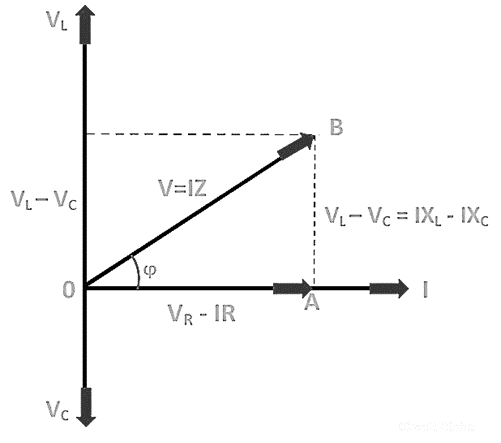
Apparatus Used:

Sl. No.	Name of the apparatus	Quantity	Specification	Makes name
1.	Single phase variac	1	230/0-270 V ac
2.	LCR Trainer Kit	1		Sushama Electronics
3.	Digital Multimeter	3	0-750 V, 10 A	Akademika
4.	Wattmeter	1	Digital
5.	LCR Meter	1	Digital	Metravi
6.	Connecting Probes	10		RGP-2

Remarks:

1. The phasor diagram of different voltage and current for at least two observation are drawn in the graph paper.
2. The value of power factor and magnitude of the supplied voltage are found from phasor diagram.