Verification of KCL & KVL

Experiment No.: 3

Experiment Name:

Verification of Kirchhoff’s Current Law and Kirchhoff’s Voltage Law.

Objective:

1. To verify Kirchhoff’s Current Law
2. To verify Kirchhoff’s Voltage Law

Theory:

Kirchhoff’s Current Law : The algebraic sum of current at any junction of a system of conductors is zero, i.e. the sum of the currents flowing into a junction must be equal to the sum of current flowing away from the junction.

Kirchhoff’s Voltage Law : In a closed electric circuit the algebraic sum of potential drops is equal to the algebraic sum of total electromotive force occuring round the circuit.

Circuit Diagram:

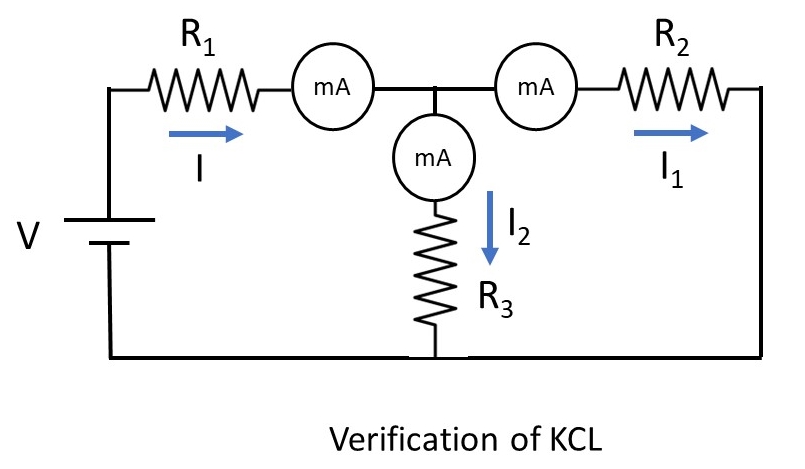
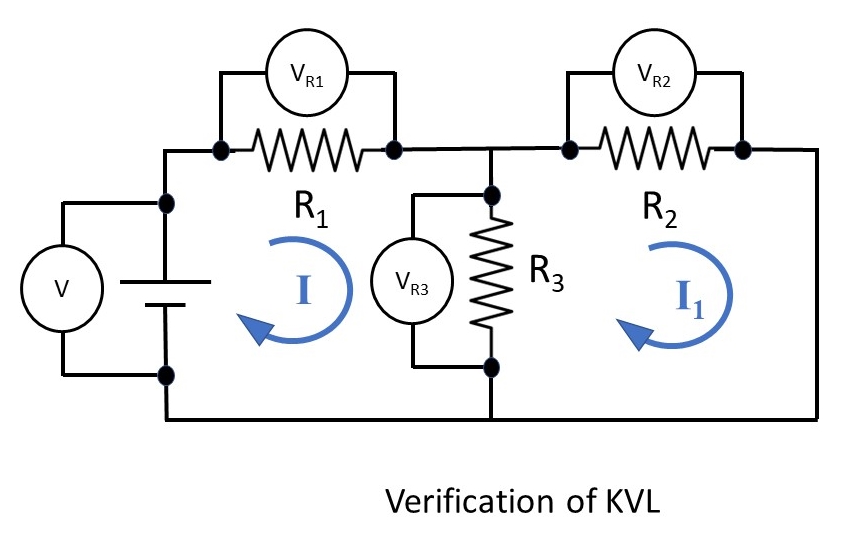
Procedure:

KCL:

1. Connect the circuit in the trainer kit as per the circuit diagram
2. Adjust the input voltage by adjuster for different reading
3. Connect the ammeters to get the respective currents meeting at the required node
4. Repeat the same procedure for different observation
5. Compare the value with theoretical results

KVL:

1. Connect the circuit in the trainer kit as per circuit diagram
2. Adjust the input voltage by adjuster for different reading
3. Connect the voltmeters to get the required voltage
4. Repeat the same procedure for different observation
5. Compare the value with theoretical results

Observation Table:

KCL:

Input Supply Voltage (V)	I1 (mA)	I2 (mA)	Total Current, I (mA) [measured value]	Total Current, I (mA) [theoretical value]
7	4.66	4.64	9.4	4.66+4.64 = 9.3

KVL:

Loop No.	Supply Voltage, V (V)	VR1 (V)	VR2 (V)	VR3 (V)	Algebraic sum of voltages (V) [measured value]	Algebraic sum of voltages (V) [theoretical value]
1	9.68	6.58		3.25	6.58+3.25 = 9.83	9.68
2			3.143	3.09	3.143-3.09 = 0.053	0

Apparatus Used :

Sl. No.	Name of the apparatus	Quantity	Specification	Maker’s Name
1.	Network theorem trainer kit- 1	1		M.E.W.
2.	Digital Multimeter	2	0-500-700 V, 10 A	Akademika
3.	Connecting Probs	10		RGP-2

Remarks:

We have compared the measured values with the theoretical results. The measured values are a little diviated from the theoretical values. Thus the KCL and KVL is verified successfully.