Experiment No.: 3
Experiment Name:
Use two watt-meters for measuring active power of three-phase balanced load.
Objective:
To use two watt-meters for measuring active power of three-phase balanced load.
Theory:
For Balance Load Condition:
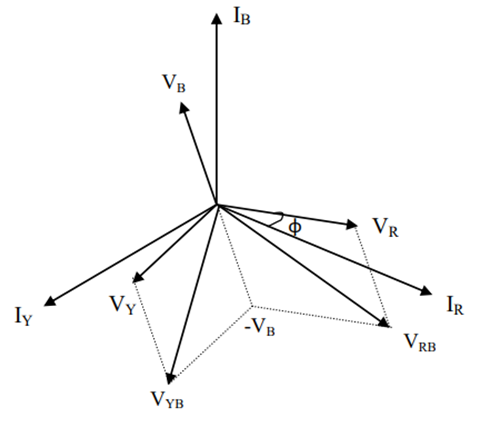
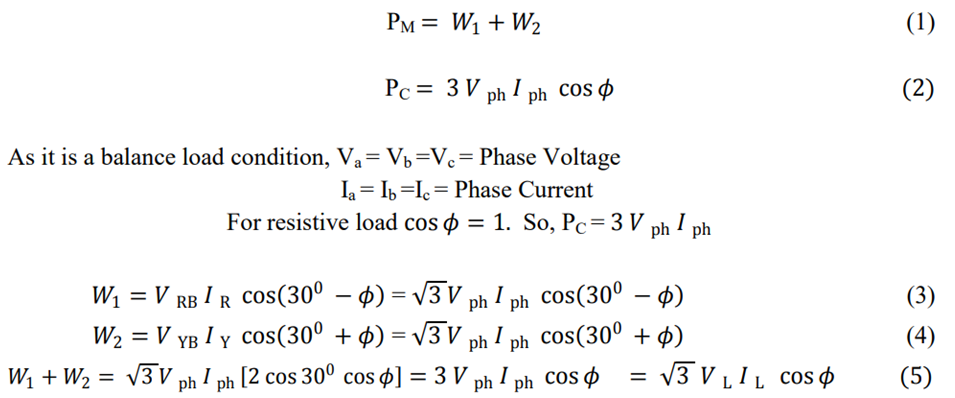
The above equation shows that the sum of the two wattmeter readings gives the total power consumed in the three-phase balanced system. We can also calculate the load power factor angle from the measurement of W1 and W2.
Circuit Diagram:
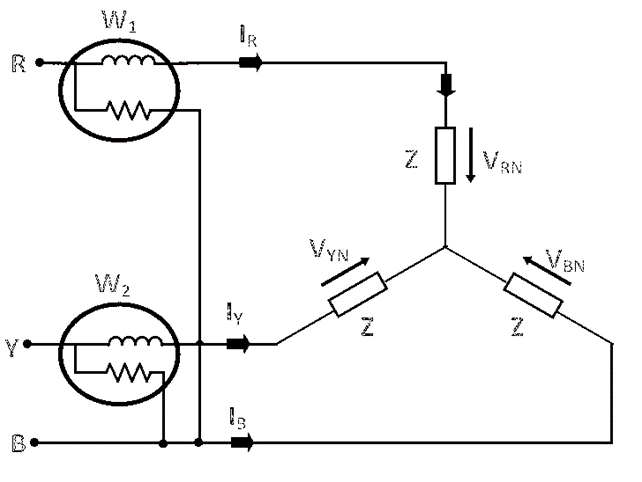
Procedure:
- Make the connections as per the circuit diagram.
- Switch on A.C supply.
- For balanced load condition measured the values of wattmeters, ammeters and voltmeter.
- Switch off all the loads and supply.
Observation Table:
| Sl. No. | Condition | Load type | M.F. | W1 (W) | W2 (W) | W = W1+W2 (W) | cos Φ | Φ |
| 1. | Balanced load | Resistive Load | 2 | 320×2 = 640 | 360×2= 720 | 1360 | 0.995 | 5.817 |
| 2. | Balanced load | Resistive Load | 2 | 760×2= 1520 | 720×2= 1440 | 2960 | 0.998 | 2.68 |
Calculation:
cos Φ = cos (tan-1 √3. (W2-W1)/(W2+W1)) = 0.995
Apparatus used:
| Sl. No. | Name of Apparatus | Quantity | Specification | Makers name |
| 1. | Single phase wattmeter | 2 | 0-750-1500-3000 W 150-300-600 V 5-10 A, Electrodynamometer type | MECO-G |
| 2. | Three phase load box | 1 | Resistive Load |
Remarks: Effect of power factor variation on wattmeter reading.
| Φ | pf (cosΦ) | W1 | W2 |
| 0O | unity | W1 =W2 | W1 = W2 |
| 30 O | 0.866 | W1 = (W2/2) | W2 = (W1/2) |
| 60 O | 0.5 | W1 = 0 | W2 = W |
| 90 O | 0 | W1 = +W | W1 = -W |

trental cost india